巧用勾股定理 提升应变能力

巧用勾股定理 提升应变能力

韩启国

江苏省兴化市安丰初级中学 

勾股定理是初中数学中的一个重要定理，它是沟通几何与代数的桥梁，也是反映自然基本规律的一条结论．在巧用勾股定理解题时，若能正确把握数学思想，则会开阔解题思路，优化解题过程。下面举例说明勾股定理应用中蕴含的数学思想，以作参考。

一、整体思想

整体思想就是指在研究和解决数学问题时，通过研究问题的整体形式、整体结构、整体特征，从整体上认识问题、思考问题，从而对问题进行整体处理的思想方法。

例1.(2021·宾阳县期中）在RtABC 中，a、b为直角边，c为斜边．若a + b =21, c =15，则△ABC的面积是（    ）

 A . 25 C . 63 B . 54 D．无法确定

解：∵ a + b =21, c =15,∴ ( a + b )2=441，即 a2 ++2ab+b2=441．

又∵ a2 + b2 = c 2=225,∴2ab=216,∴即 S△ABC =54．故选B .

点评：本题中AC和BC的长无法直接求出，于是把AC+BC看作一个整体进行求值，其它问题便迎刃而解.可以看出，运用整体思想解题能使复杂问题简单化，难度大大降低，起到一举解决问题的作用。

二、方程思想

方程思想是指运用适当的数学语言，从问题的数量关系出发，通过设未知数，将问题中的条件转化为数学模型——方程(组)，然后运用相应的知识来求解问题的一种数学思想。

例2.(2021·黄石模拟）如图是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据： AM =4米， AB =4米， LMAD =45°, CM : CB =3:5，则警示牌的高 CD 为米．

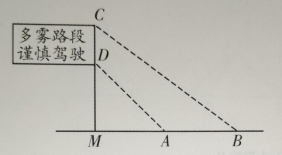
解：∵ AM =4米， ∠MAD =45°, ∴ DM =4米，∵ AM =4米， AB =4米，∴ MB =8米，

∵ CM : CB =3:5,设 CM =3a米， CB =5a米，∴ 9a2+ MB2 =25a2,∴ a =2米，∴ DC = CM - DM =2米．

点评：本题主要考查运用勾股定理构建方程，把已知量与未知量建立关系是解题的关键；同时也体现了运用方程思想解题的简便快捷。

三、数形结合思想

数形结合思想就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过抽象思维与形象思维的结合，使复杂问题简单化，抽象问题具体化的一种数学思想。

例3.(2021·无锡新吴区期中）如图所示，OA⊥OB ,OA=45cm , OB =15 cm，一机器人在B处发现有一个小球自 A 点出发沿着AO方向匀速滚向点0，机器人立即从B处出发以相同的速度匀速直线前进去拦截小球，在点C处截住了小球，则机器人行走的路程BC为cm .

解：小球滚动的速度与机器人行走的速度相等，运动时间相等，即BC = CA ，设AC = x cm ，

则OC =(45－x) cm ,在 Rt△OBC 中，由勾股定理可知 OB2 + OC2 =BC2,

又∵ OA =45cm, OB =15cm,152+(45一 X )2=X2,解得＝25,即 BC =25cm.

故如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程 BC 是25cm.

点评：本题结合勾股定理，通过构造几何图形，再利用图形中边与边的关系求出答案，充分体现了数形结合思想的优越性．其实勾股定理本身就是数形结合的定理，它的验证和应用都体现了数形结合的思想。

四、分类讨论思想

例4.在△ABC中， AB =15, AC =20, BC 边上的高线12，则△ABC的面积为．

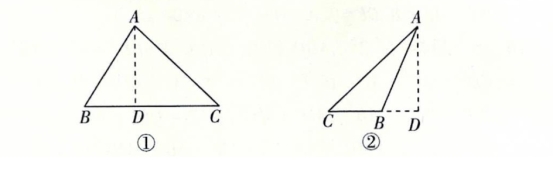
解：已知三角形两边的长和第三边的高，未明确这个三角形是钝角还是锐角三角形，所以需分情况讨论如图①，当△ABC 为锐角三角形时，高AD在三角形的内部．在Rt△ABD 中， AB =15, AD =12，由勾股定理得， BD2= AB2- AD2 =152-122=81，则 BD =9（负值舍去）．在 Rt △ADC 中 AC =20, AD =12，由勾股定理得， DC2 = AC2 - AD2 =202-122=256，则 DC =16（负值舍去）．∴ BC = BD + DC =9+16=25,∴ ．如图②，当△ ABC 为钝角三角形时，高AD在三角形的外部同①的解法相同， BC =7,．综上所述，△ABC 的面积为42或150.

分类讨论思想是指当一个数学问题所给的对象不能进行统一研究，就需要对研究对象按某个标准分类，然后对每一类分别研究，得出每一类结论，最后综合各类结果得到整个问题解答的数学思想。

点评：本题通过类比勾股定理，分两种情况作出判断，体现了分类讨论的解题思想，数学里的许多问题，在解答过程中只有用分类讨论的思想，才能保证解答完整准确，做到“不漏不重”。

五、转化思想

转化思想又叫化归思想，就是指将需要解决的问题由难化易，由繁化简，从而实现化未知为已知的数学思想。

例5.(2021·济南月考）如图，在△ ABC 中， AB =9, AC =6, AD 1 BC 于D , M为AD上任意一点，则MB2 - MC2的值为．

解：在Rt △ABD和Rt△ADC 中， BD2 = AB2 - AD2 , CD2 = AC2 - AD2．在Rt△BDМ和Rt△CDM 中，BM2= BD2+ MD2= AB2 - AD 2+ MD2, MC2 = CD 2+ MD2= AC2 - AD2 + MD2 . ∴ МB2- MC2 =( AB2 -AD2 + MD2)-( AC2 - AD2 + MD2)= AB2 -- AC2 =45.

例6.如图，四边形ABCD和四边形AEFG都是正方形，点B在 EF 上，若S 1=140,S2=124，则EB的长为．

解：设△ABE的面积为S . ∴S正方形 ABCD = S + S1 = S +140，

　　　　　　　　　        S正方形 AEFG = S + S2= S +124，而 S正方形 ABCD =AB2，S正方形 AEFG = AE2，

∴AB2－AE2= 140－124＝16，∴BE =4.

点评：本题BE很难直接求得，将其转化为正方形ABCD与正方形AEFG的面积差是关键。由此可见，转化策略是数学解题中一种常用的思想方法，可以说，数学解题的过程实际就是问题转化的过程。

总而言之，巧用数学思想方法是随着学生对数学知识的学习、运用逐渐形成的，它是数学知识的精髓，是把知识转化为能力的桥梁，同时也是对数学内容的一种本质认识。在运用勾股定理解决问题的过程中，如果能巧妙地抓住思想方法，就抓住了问题的本质，从而提升了解题的应变能力。

邮编：225766   地址：江苏省兴化市安丰初级中学  韩启国