湖南科技学院理学院 湖南永州, 425199
摘要:本文基于偏微分方程有限元法求解原理,运用Matlab中的偏微分方程工具箱(PDE Toolbox)对三类典型的二阶偏微分方程:椭圆型方程、双曲线型方程和抛物线型方程算例进行求解,为求解偏微分方程的提供参考。
关键词:偏微分方程,有限元,Matlab偏微分方程工具箱
0 引言
偏微分方程定解问题是描述许多自然现象或工程问题的最重要的数学模型,应用非常广泛[1]。解析法只能求解非常简单的偏微分方程,远远不能满足科学研究和工程实际的需要。随着计算机技术和科学计算的迅速发展,数值解法成为求解偏微分方程的重要工具[2-3]。数值解法将连续问题离散化,最后将偏微分方程化成线性代数方程组。根据离散化方法不同,偏微分方程数值解法主要有差分法和有限元法。有限元法是分片定义试函数与变分原理相结合的产物。它能适应各种形状的区域,且通用性强,现已成为求解偏微分方程定解问题的一种有效数值方法[4]。本文首先简述了偏微分方程有限元法原理,然后,对Matlab中的偏微分方程工具箱(Partial Differential Equations Toolbox)的功能和求解思路进行了阐述[5-6],最后,给出了用PDE Toolbox求解椭圆方程、、双曲线方程和抛物线方程的计算实例。
1 偏微分方程有限元法原理
偏微分方程有限元法的基本思想是将实际上连续的整个求解域进行离散化处理,即用一些假想的面或线将求解域分割为一系列的单元,各个单元之间仅在有限个节点处相互连接。取未知函数的节点值作为基本未知量,在每个单元上选取一个近似的插值函数表示单元中场函数的分布规律。利用变分原理来获得单元的刚度方程,然后按一定的规则把所有单元的刚度方程组集合起来,经适当的边界条件处理,便得到整个系统的总体方程组。这样,偏微分方程便转化为一组常微分方程。最后,求解总体方程组,得到节点值和用插值函数确定整个求解域上的场函数。
2 PDE Toolbox功能与求解过程
2.1 PDE Toolbox 功能
Matlab软件中的偏微分方程工具箱(PDE Toolbox)提供了用有限元方法求解二维偏微分方程的实用工具,它可以求解以下三类偏微分方程定解问题。
(1)椭圆型方程
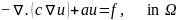 (1)
(1)
(2)抛物线型方程
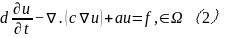
(3)双曲型方程
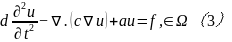
其中 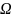 是平面内有界区域,
是平面内有界区域,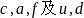 是定义在
是定义在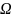 上的函数。
上的函数。
微分方程边界条件可为:
(1)狄利克雷边界条件(Dirichlet)
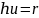 (4)
(4)
(2)诺依曼边界条件(Neumann)
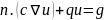 (5)
(5)
其中 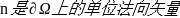 ,
, 是定义在
是定义在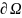 上的函数。
上的函数。
(3)混合边界条件
它由狄利克雷边界条件和诺依曼边界条件混合组成。
在Matlab工作空间命令行中输入pdetool,系统立即启动偏微分方程工具箱(PDE Toolbox)图形用户界面(GUI),然后就可以绘制定解区域,设置方程和边界条件,剖分网格,求解,最后可视化计算结果。另外,也可用M文件调用PDEToolbox中的命令函数编程求解偏微分方程。
2.2 求解步骤
用偏微分方程工具箱(PDE Toolbox)图形用户界面(GUI)求解偏微分方程的一般步骤是
(1)定义求解几何区域;(2)设置边界条件;(3)设定偏微分方程类型及系数;(4)化分网格;(5)求解;(6)计算结果后处理。
3 用PDEToolbox求解典型二阶偏微分方程算例
3.1 求解椭圆型方程的算例
[算例1] 单位圆上泊松方程的边值问题:

在PDE Toolbox图形用户界面中,先绘制圆形求解域并设置圆心坐标为(0,0),半径为1。选择Dirichlet边界条件,h=1,r=x。选择方程类型为Elliptic,c=1,a=0,f=-12。然后,进行网格化分,生成541个节点,1016个三角形单元数。最后,求解方程,计算结果如图1所示。
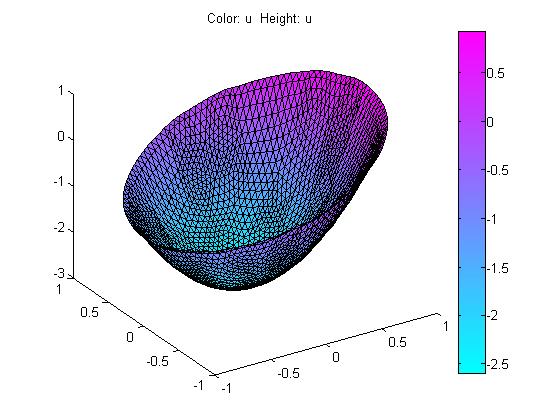
图1 数值计算结果
该问题的解析解为
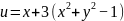 (7)
(7)
数值解与解析解的绝对误差如图2所示 。
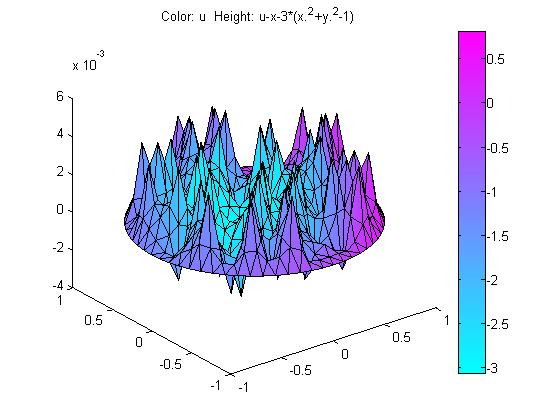
图2 数值解与解析解的绝对误差
由图2可知,整体来看,数值解与精确解误差很小,在边界处误差为零。
3.2求解双曲线型方程的算例
[算例2] 求解二维波动方程:
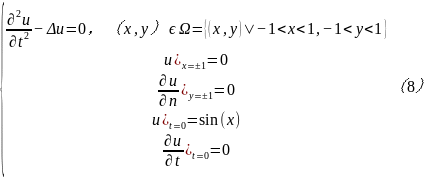
在PDE Toolbox图形用户界面中,先绘制正方形求解域并设置四个角点坐标分别为(-1,-1),(-1,1),(1,1),(1,-1),。设置左右边界为Dirichlet边界,h=1,r=0,上下边界为Neumann边界,q=0,g=0。选择方程类型为Hyperbolic,c=1,a=0,f=0,d=1。然后,进行网格化分,生成665个节点,1248个三角形单元数。在求解参数中,设置时间,Time=linspace(0,5,10),设置u的初始值u(t0)为sin(x),u'的初始值为0,并设置解的允许相对误差和绝对误差;最后求解方程,计算结果如图3所示。
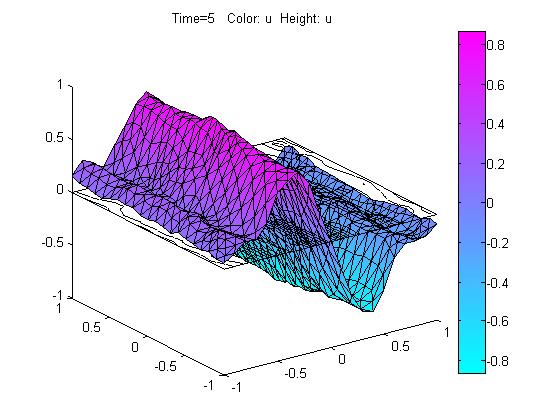
图3 数值计算结果
3.3求解抛物线型方程的算例
[算例3] 求解单位正方形区域齐次热传导方程:

在PDE Toolbox图形用户界面中,先绘制正方形求解域并设置四个角点坐标分别为(-1,-1),(-1,1),(1,1),(1,-1)。设置左边界为Dirichlet边界,h=1,r=100,右边界为Neumann边界,q=0,g=-20。其它边界选为Neumann边界,q=0,g=0。选择方程类型为Parabolic,c=1,a=0,f=0,d=1。然后,进行网格化分,生成177个节点,312个三角形单元数。在求解参数中,设置时间,Time= 0:10,设置u的初始值u(t0)为0;最后求解方程,计算结果如图4所示。
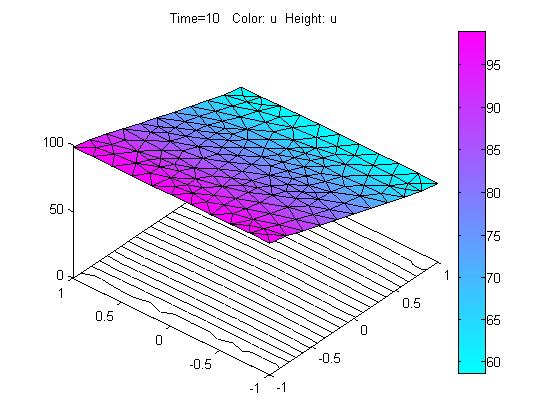
图4 数值计算结果
4结论
论文运用Matlab中的偏微分方程工具箱(PDE Toolbox)对二阶偏微分方程算例进行了有限元求解,表明Matlab偏微分方程工具箱数值计算结果精度好,可视化方便,可为求解偏微分方程提供参考。
参考文献
[1] 卓金武,王鸿钧,MATLAB数学建模方法与实践(第3版) 北京航空航天大学出版社,2018
[2]李荣华,刘播,微分方程数值解法(第4版)[M], 北京:高等教育出版社,2009
[3]王秀喜,吴恒安,计算力学基础[M],合肥:中国科学技术大学出版社,2009
[4] 李开泰,黄艾香,黄庆怀,有限元方法及其应用[M],北京:科学出版社,2021
[5] 陆君安,尚涛,谢进,谷平,偏微分方程的Matlab解法[M], 武汉:武汉大学出版社,2001
[6] The MathWorks inc.,Partial Differential Equation Toolbox For Use with Matlab, 2011