新方法绘制四维空间坐标和对坐标点的理解——四维坐标及其点的表示和弹缩坐标的构想

新方法绘制四维空间坐标和对坐标点的理解——四维坐标及其点的表示和弹缩坐标的构想

白宁宁

迎招书院附属外协技术

摘要：四维空间一直很神秘，我们处在三维空间中，很少能感知四维空间，面体结构如何形成[1]，面体结构是否真的存在，物理方法，推理出面体结构，是找到了进入多维空间的大门。我们可以从坐标的形成方式，来推理，我们熟悉了四维坐标的形成过程，推理面体结构，对于掌握应用四维坐标构图也就不是很远了，下面我们介绍一下坐标面体结构另一种理解运用和多维空间的坐标建立，即为弹缩坐标。

关键词:四维空间 坐标 弹缩坐标

在谈论空间维度，有人说空间是11维的，有的人说空间是12维的，空间到底是多少维的，等我做完图，就可以得到答案。

1四维坐标的建立

从零维开始，我们看推理过程。

零维：点，用笔画，时间可能非常少，测量时间T0，匀速延长时间0。

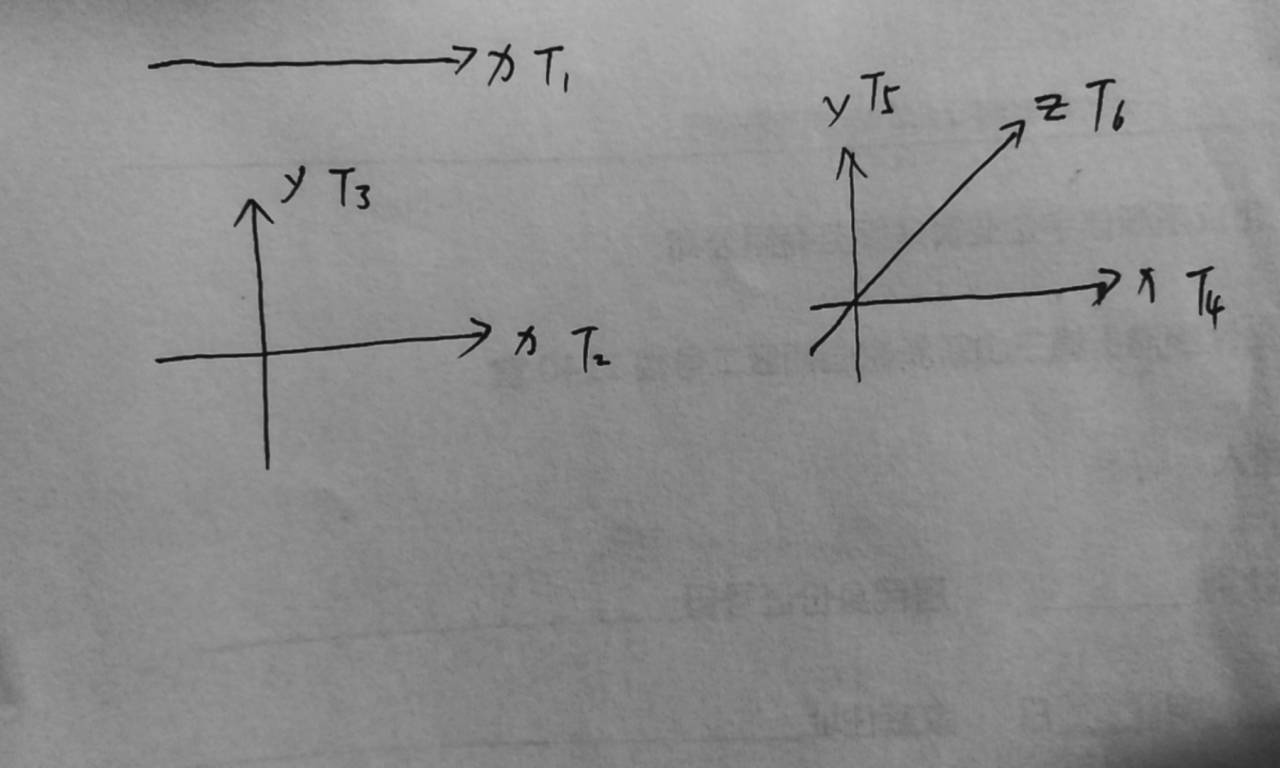
一维：直线，X，用笔画，测量点时间为T1 ，匀速时间延长为T11

二维：平面直角坐标系，XY，用笔画，X测量点时间为T2，匀速时间延长为T12，Y测量时间点为T3，匀速时间延长为T13，直角坐标系点T2 和点T3的匀速时间复合得到。

三维：直角坐标系（笛卡尔坐标系），XYZ，X测量时间点为T4，匀速时间延长为T14，Y测量时间点为T5，匀速时间延长为T15，Z测量时间点为T6，匀速时间延长为T16，坐标系是点T4，T5，T6复合，匀速时间复合得到。

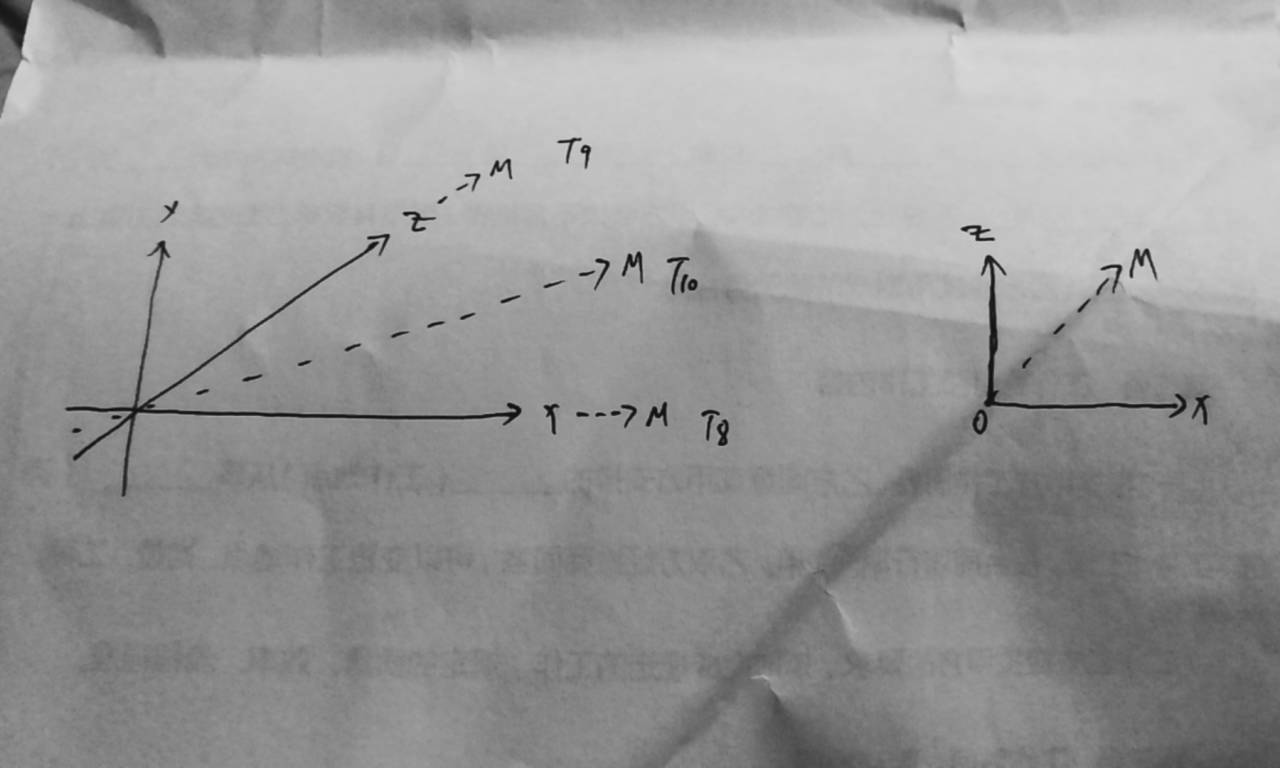
四维：空间直角坐标系，我们先看直角坐标系（笛卡尔坐标系），坐标轴过原点，分别互相垂直，是时间与时间点的复合，那在面上找一个数轴，在匀速时间下，互相垂直下时间点的缩合，这样不就可以了吗，答案是有的。我们看这个M数轴，假设OM过原点，是一个以O为圆心，在XOZ面上转动的直线，T8时，OM与X轴重合，这时候，OM垂直于Y轴，垂直于Z轴，T9时，OM与Z轴重合，OM垂直于Y轴，垂直于X轴，T8与T9缩合成为T10，出现与X轴重合的OM垂直X轴，与Z轴重合的OM垂直于Z轴，取出XOZ面，出现，角XOZ是90度，角XOM是90度，角MOZ是90度，把这个面放在三维空间中，这是一个长方形或正方形的三个面，这是一个面体结构，四维空间的一个面，三维空间的一个体，面体结构还原，这样看，四维坐标主结构是笛卡尔坐标T4，T5，T6，加上一个缩合时间T10复合得到。

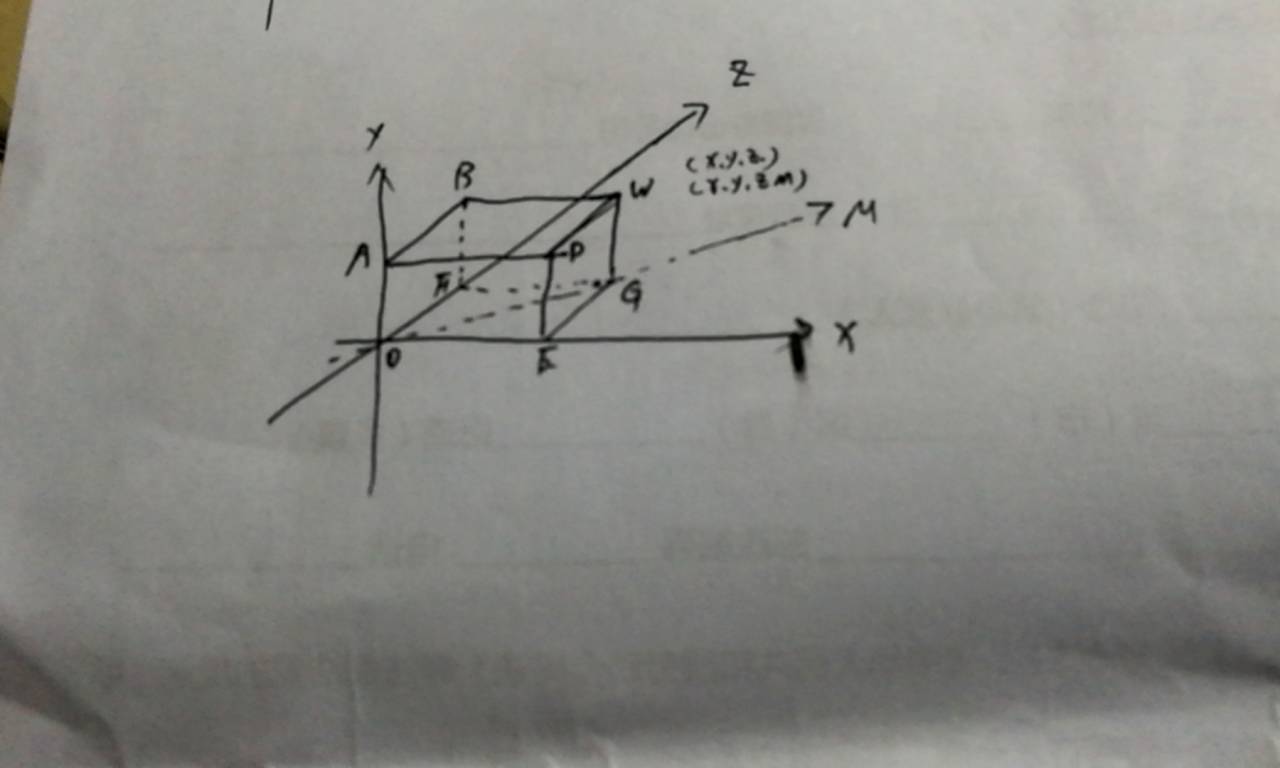
2点的表示意义（X，Y，Z，M）

（X，Y，Z，M）在坐标中，假设存在一个正方体，OEGF-ADWB，三维W点坐标为（1，1，1）假设它为面体结构，把它压回面体结构中即为面XOZ中，再以O点转动回来，是Y轴的高度改变了，第二次转回来，M表示的是四维当中Y的刻度，这个过程我们称为坐标的弹性伸缩，在四维空间中，存在（1，1，1，1）这样的坐标，包含了面体结构可能的活动范围，M对应的1，是面体结构，由平面体到体的伸缩，面体在三维体Y轴上伸缩的数值为M，我们再代入距离公式|e| = (a^2+b^2+c^2+d^2)^1/2：OE的平方加EG的平方，开根号为OG长度，OG平方加WG的平方，开根号为OW的长度，OW压回面体结构，OW的平方加上Y轴对应的长度（M坐标长度）平方，开根号，为四维坐标点到原点距离。即为|e| = (a^2+b^2+c^2+d^2)^1/2＝2

3讨论

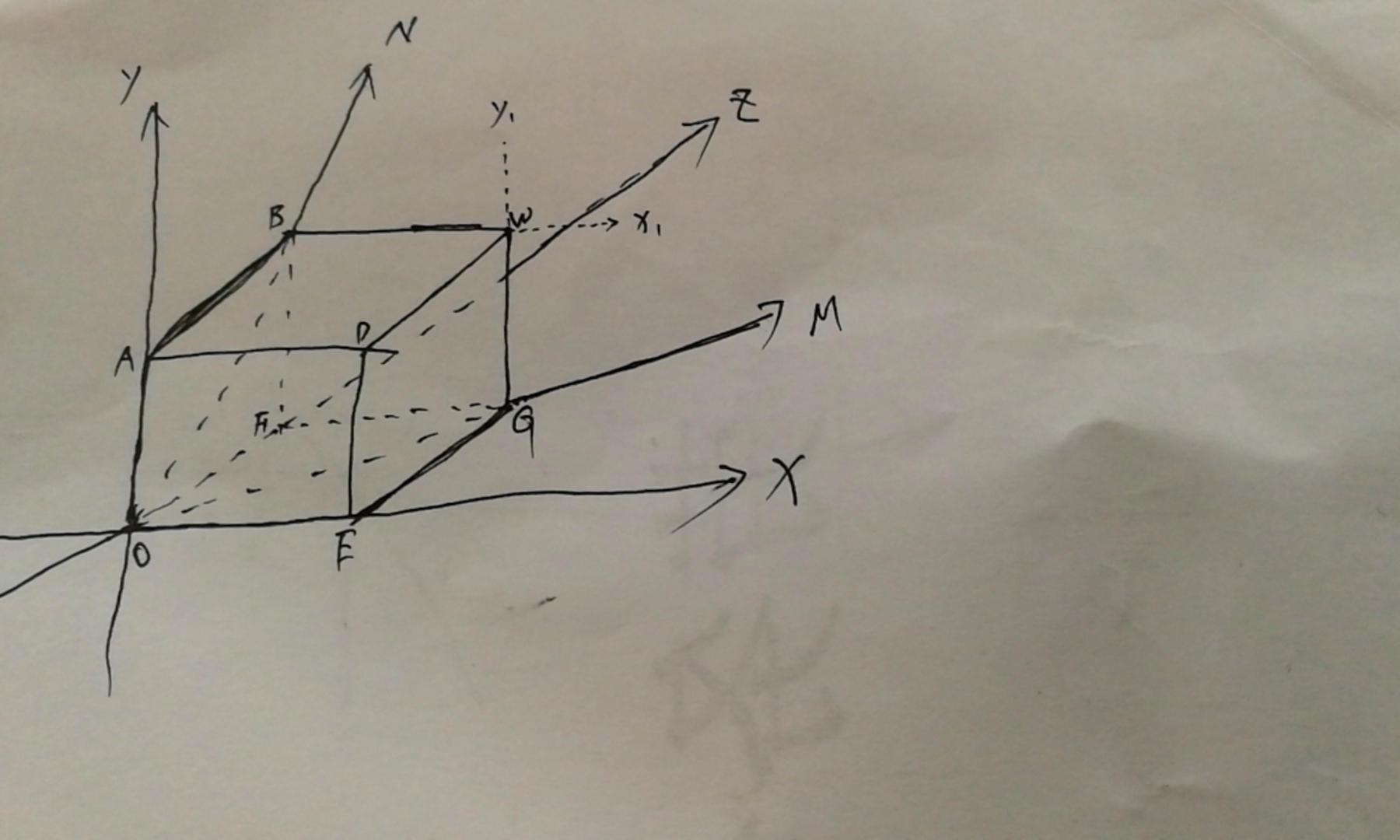
弹缩坐标的定义：假设存在如下图片

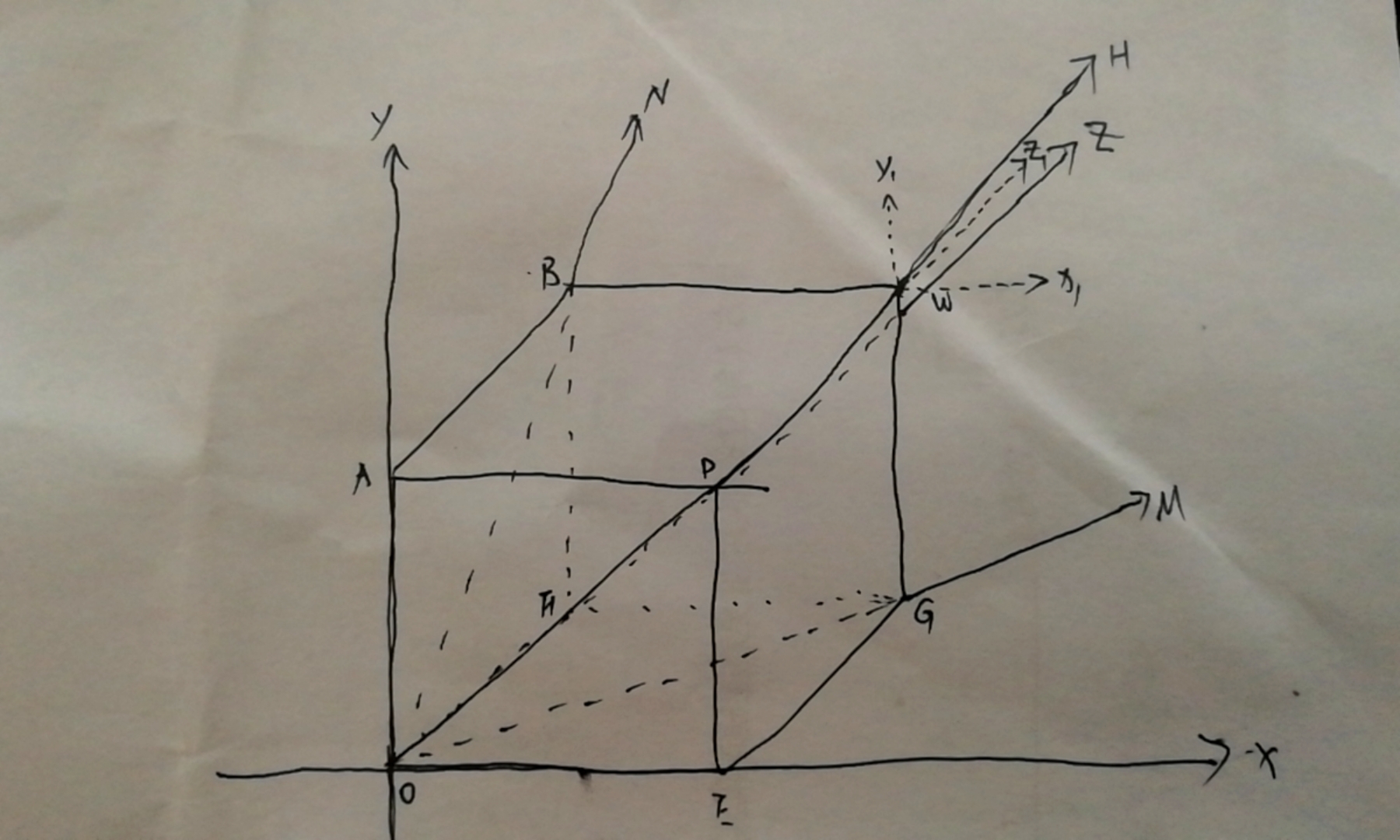
假设我们把四维空间OEGF—ADWB复合到坐标O-XYZ当中，以OFGE为面体结构，它的伸缩坐标对应的是Y，以OABF为面体结构，它的伸缩坐标对应的是X，以OEDA为面体结构，它的伸缩坐标对应的是Z，以W为原点，建立伸缩坐标W-X1Y1Z1，我们称它为一级弹缩坐标，在三维空间上，W可能与坐标原点O，是重合的。

坐标从一维到四维，貌似有一些规律，我们再看一下五维坐标可能的建立方法。四维点的表示是（X，Y，Z，M），假设面体结构存在于面XOZ，三维数轴为对应的Y值，弹缩数轴对应的是Y1。

五维点的表示是（X，Y，Z，M，N），我们开始做图，让N过原点落在面AOF面上，同理用时间缩合复合的方法，可以得到下面这张图：

五维（X，Y，Z，M，N）这当中，N对应的是X数轴，弹缩数轴是X1，M对应的是Y数轴，弹缩数轴是Y1。 三维空间中，W与O可能是重合的。

六维点的表示为（X,Y,Z,M,N,H）我们开始做图，让H过原点，落在OXY面上，同理用时间复合缩合的方法，得到。

我们看到，面体结构OEGF对应的弹缩数轴为，Y1，面体结构OFBA对应的弹缩数轴为X1，面体结构OEDA对应的弹缩数轴为Z1。弹缩坐标W-X1Y1Z1，三维当中W与O可能是重合的。

如果多维空间坐标可以这样制作，坐标系实际上是时间下的数轴复合缩合过程，维数多的话，我们可以用一级弹缩坐标，和二级弹缩坐标复合缩合表示，每超出三个弹缩数轴，可以生成一个弹缩坐标，如果能做出12维度以上的坐标轴，即为一个三维笛卡尔坐标加上三套弹缩坐标既可以得到，这样的话，宇宙不是12维度，可能有更多维度，但是很有规律可寻找。

3需要解决的问题有

3.1四维空间，第四个坐标轴，是否为面积，这个数轴，是面在时间点下缩合成的，然后直接聚合成坐标轴使用的。

3.2四维空间，直角坐标系，有时间复合，这有三个匀速时间，再复合时候，有一个非匀速时间，这样有三个匀速时间和一个非匀速时间复合，这四个时间是否对体积有影响，四维空间是非匀速时间下，在匀速时间里测量体积，有点类似密度，同体积的物体，在三维空间中，密度发生变化，三维中体积变大。

3.3这里提到的六维坐标是否为实际上的四维坐标还有待证实。

3.4 数学公式对坐标的推理论证，知道坐标的构建过程，可以从坐标的形成过程开始论证，也可以从坐标上由公式由易到难论证，先论证两点距离，点线距离，点面距离，周长，面积，体积，超体积公式论证。也可以结构和公式分步论证同时进行。如果公式符合，才应该是，这是当前需要解决的问题。

参考文献：

[1]李科.让四维空间不再神秘[J].时代教育,2014,(13)：160-171.