江苏省 宜兴市丁蜀高级中学
摘要:在进入二轮微专题复习阶段,是学生提升思维能力、解题能力的关键时期。本文以高三二轮复习中“与圆有关的最值”这一微专题为例,对如何采取教略而学丰,精略有致的方法构建高中数学“深度学习”课堂,进行了初步的尝试和探析。在课堂环节的设计上主要分:‘提问设疑、顺应---问题推动、引入---适时探究、深入’这三个环节展开。
关键词:深度学习、课堂构建、深度思维
正文:
本文以高三二轮复习中“与圆有关的最值”这一微专题为例,对如何采取教略而学丰,精略有致的方法构建高中数学“深度学习”课堂,进行了初步的尝试和探析。
一、提问设疑,顺应学生思维模式,展开教学内容
“深度学习”的第一步是如何引导学生展开自主研学,问题情境引导是最常用的导入方法之一。在教学过程中,教师应站在学生的角度,顺应大多数学生的思考方式来提出问题。
在微专题“与圆有关的最值”这一课,主要围绕圆外一点和圆内一点的相关最值问题展开。鉴于学生对求两点之间距离是比较熟悉的,所以从学生熟悉的内容为切入点,由如下问题展开了本课的内容。
点在圆外篇:
问题1:已知P(1,0),Q为圆C: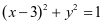 上任一点,则
上任一点,则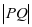 的最小值为.
的最小值为.
生1:设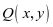 ,则
,则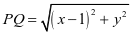 ,由圆方程知:
,由圆方程知: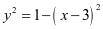 ,代入得
,代入得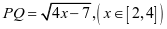 ,可求得最小值为1.
,可求得最小值为1.
生2:数形结合,可知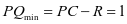 .
.
师:若将点P的坐标改为P(1,1),Q为圆C: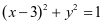 上任一点,则
上任一点,则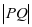 的最小值?
的最小值?
生:用数形结合比较简单.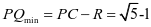 .
.
师:生1选用代数的方法将PQ的最值问题转化为一次函数的最值很好地解决了问题1,但对于变题,此种方法明显没有数形结合来得简捷.对于处理和圆上动点有关的最值问题,采取数形结合,变抽象为具体,不失为一条有效途径.
二、问题推动,串成一线,层层引入
在问题1的基础上,将圆外一定点改为圆外一动点,由两点之间距离的最值逐层铺垫展开,引入切线段长和面积的最值问题。由定到动,由线长到面积。
问题2:若P为直线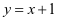 上任一点,Q为圆C:
上任一点,Q为圆C: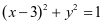 上任一点,则
上任一点,则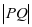 的最小值为 ;
的最小值为 ;
师:点P由圆外一定点改为了直线上的一个动点,该如何解决呢?
生:不妨将点P固定,则可以把问题转化为求圆C外一定点P到圆C上的点Q的最小值问题。
显然当C、Q、P三点共线时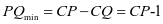 ,所以当
,所以当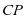 最小时,
最小时,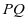 最小.当
最小.当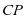 垂直于直线
垂直于直线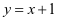 时,
时,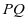 最小.
最小.
师:想法非常好。利用先定而后动,数形结合巧妙地解决了多动点问题。这种方法也经常用于求解析几何中的多动点最值问题。
问题3:若P为直线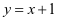 上任一点,由点P向圆C:
上任一点,由点P向圆C: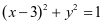 引切线,则切线长的最小值为 ;
引切线,则切线长的最小值为 ;
问题4:若P为直线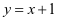 上任一点,由点P向圆C:
上任一点,由点P向圆C: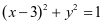 引切线,所作切线为PA,PB,A、B为切点,则四边形PACB面积的最小值为 ;
引切线,所作切线为PA,PB,A、B为切点,则四边形PACB面积的最小值为 ;
学生通过分析,透过问题的表象,很快就寻找到了问题的根源,发现了这两题和上题的联系。
三、适时探究,凸显重难点,引导思维逐步深入
讲解是课堂教学中重要的一个环节。然而该如何讲,讲多少,讲什么都是需要考虑的问题。教师在课堂教学过程中,通过适当的提问、启发、讲解,引导学生展开深度的自主探究,引导其思维逐步深入。
问题5:若P为直线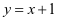 上任一点,由点P向圆C:
上任一点,由点P向圆C: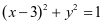 引切线,所作切线为PA,PB,A、B为切点,当PC= 时,
引切线,所作切线为PA,PB,A、B为切点,当PC= 时,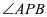 最大;
最大;
师:大家可以谈谈自己的解题思路吗?
生1:由图像结合对称性可知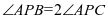 .所以这个问题其实就是求
.所以这个问题其实就是求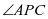 的最大值。
的最大值。
师:不错,那接下去如何求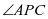 的最大值呢?
的最大值呢?
这时候有一部分同学就卡在那儿没声了。
师:角的最值往往通过三角函数的最值来求得,大家通过观察图像,看看选用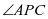 的哪个三角函数值比较好呢?
的哪个三角函数值比较好呢?
生2:选用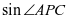 比较好。
比较好。
师:能说一下选择正弦函数的理由么?
生2:因为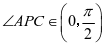 ,正弦在这个范围内单调递增,所以当
,正弦在这个范围内单调递增,所以当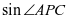 最大时,也就是
最大时,也就是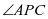 最大。
最大。
师:很好。这种想法很合理。不过正切函数在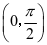 上也是单调递增的,为什么不选它呢?
上也是单调递增的,为什么不选它呢?
生3: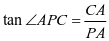 ,
,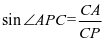 ,两者相比较,
,两者相比较,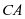 为定值
为定值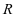 ,
,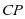 中
中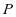 为动点,而
为动点,而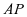 两个都是动点,显然
两个都是动点,显然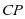 的最值更容易求。要求
的最值更容易求。要求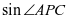 最大,也就是
最大,也就是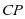 最小,其实就是上面的问题2.
最小,其实就是上面的问题2.
通过这一系列的提问,对学生的思维进行适当的点拨,让这些看似孤立的、分散的内容在这些问题的层层递进下,利用数形结合构建起解决这类问题的通性通法。让学生真正学会如何做、理解为什么这么做。
四、方法提炼,思维渗透,提升能力
正所谓牵一发而动全身,让学生学会发散性思维,启发问题意识,能对同一问题进行多层面、多角度进行思考,学会由表及里地进行思考分析问题。
能力提升篇:
问题:已知P是圆C: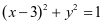 上的动点,Q是y轴上的动点,A(1,2)为定点,则
上的动点,Q是y轴上的动点,A(1,2)为定点,则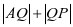 的最小值为 ;
的最小值为 ;
变1:若点P在抛物线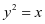 上,点Q 在圆C:
上,点Q 在圆C: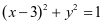 上,则
上,则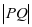 的最小值为
的最小值为
变2:已知圆C: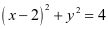 ,设圆M的方程
,设圆M的方程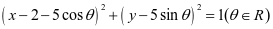 ,过圆M上任意一点P作圆C的两条切线PE、PF,切点为E,F,则
,过圆M上任意一点P作圆C的两条切线PE、PF,切点为E,F,则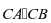 的最小值为 。
的最小值为 。
这类解析几何中的多动点问题,一直是学生的难点。指导学生利用数形结合的方法,结合图像特征,寻找题中变量与定量间的联系,化动为静解决问题。
“深度学习”课堂是师生共同探讨的一种高效课堂,让学生在课堂中充分发挥其个性特征和主观能动性。意在培养学生深度学习的能力,让学生掌握高效学习的方式,学会深度思考,提升知识应用能力。教师需要做的是精心设计教学问题与解题策略,精心调适教学互动,精心规划探究步调,真正做到“深入、深究、深刻、深远”,帮助学生提升数学素养,促进其高阶思维的发展。